Field Theory

Archived Posts from this Category

February 15, 2009

A Brief Introduction to Instantons

Posted by lanzr under Field Theory
1 Comment 

This brief instroduction is based on David Tong’s TASI Lectures on Solitons Lecture 1:Instantons.

We’ll first talk about the instantons arise in SU(N) Yang-Mills theory and then explain the connection between them and supersymmetry. By the end we’ll try to explain how string theory jumps in this whole business.

Instantons are nothing but a special kind of solution for the pure SU(N) Yang-Mills theory with action S=\frac{1}{2 e^2}\int d^4x Tr F_{\mu\nu}F^{\mu\nu}. Motivated by semi-classical evaluation of path integral, we search for finite action solutions to the Euclidean equations of motion, \mathcal{D}_{\mu} F^{\mu\nu}=0. In order to have a finite action, we need field potential A_{\mu} to be pure gauge at the boundary \partial R^4=S^3, i.e. A_{\mu}=ig^{-1}\partial_{\mu}g.

Then the action will be given roughly by a surface integral which depends on the third fundamental group of SU(N), given by \Pi_3(SU(N))=k, k is usually called the charge of the instanton. For the original action to be captured by this number k, we need to have self-dual or anti self-dual field strength.

A specific solution of k=1 for SU(2) group can be given by A_{mu}=\frac{\rho^2(x-X)_{\nu}}{(x-X)^2((x-X)^2+\rho^2)}\bar{\eta_{\mu\nu}}^i(g\sigma^i g^{-1}) where Xs are coordinate parameter \rho is scale parameter and together with the three generator of the group, we have 8 parameters called collective coordinates. \eta is just some matrix to interwine the group index i with the space index \mu.

For a given instanton charge k and a given group SU(2), an interesting question is how many independent solutions we have. The number is usually counted by given a solution A_{\mu}and we try to find how many infinitisiaml perturbation of this solution \delta_\alpha A_\mu, known as zero modes, \alpha is the index for this solution space, usually called moduli space.

When we consider a Yang-Mills theory with an instanton background instead of a pure Yang-Mills theory. We’d like to know if we still have non-trivial solutions, and especially if these solutions will give rise to even more collective coordinates. This is where fermion zero modes and supersymmetry comes in. For \mathcal{N}=2 or 4 supersymmetry in D=4, it’s better to promote the instanton to be a string in 6 dimentiona or a 5 brane in 10 dimensions respectively. The details of how to solve the equation will be beyond the scope of this introduction, and We’ll refer the reader to the original lecture notes by David Tong.

 

February 7, 2009

The spin connection

Posted by Sparticles under Field Theory
[4] Comments 

I’ve been spending some time thinking about spinors on curved spacetime. There exists a decent set of literature out there for this, but unfortunately it’s scattered across different `cultures’ like a mathematical Tower of Babel. Mathematicians, general relativists, string theorists, and particle physicists all have a different set of tools and language to deal with spinors.

Particle physicists — the community from which I hail — are the most recent to use curved-space spinors in mainstream work. It was only a decade ago that the Randall-Sundrum model for a warped extra dimension was first presented in which the Standard Model was confined to a (3+1)-brane in a 5D Anti-deSitter spacetime. Shortly after, flavor constraints led physicists to start placing fields in the bulk of the RS space. Grossman and Neubert were among the first to show how to place fermion fields in the bulk. The fancy new piece of machinery (by then an old hat for string theorists and a really old hat for relativists) was the spin connection which allows us to connect the flat-space formalism for spinors to curved spaces. [I should make an apology: supergravity has made use of this formalism for some time now, but I unabashedly classify supergravitists as effective string theorists for the sake of argument.]

One way of looking at the formalism is that spinors live in the tangent space of a manifold. By definition this space is flat, and we may work with spinors as in Minkowski space. The only problem is that one then wants to relate the tangent space at one spacetime point to neighboring points. For this one needs a new kind of covariant derivative (i.e. a new connection) that will translate tangent space spinor indices at one point of spacetime to another.

By the way, now is a fair place to state that mathematicians are likely to be nauseous at my “physicist” language… it’s rather likely that my statements will be mathematically ambiguous or even incorrect. Fair warning.

Mathematicians will use words like the “square root of a principle fiber bundle” or “repere mobile” (moving frame) to refer to this formalism in differential geometry. Relativists and string theorists may use words like “tetrad” or “vielbein,” the latter of which has been adopted by particle physicists.

A truly well-written “for physicists” exposition on spinors can be found in Green, Schwartz, and Witten, volume II section 12.1. It’s a short section that you can read independently of the rest of the book. I will summarize their treatment in what follows.

We would like to introduce the a basis of orthonormal vectors at each point in spacetime, 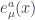e^a_\mu(x), which we call the vielbein. This translates to `many legs’ in German. One will often also hear the term vierbein meaning `four legs,’ or `funfbein’ meaning `five legs’ depending on what dimensionality of spacetime one is working with. The index \mu refers to indices on the spacetime manifold (which is curved in general), while the index a labels the different basis vectors.

If this makes sense, go ahead and skip this paragraph. Otherwise, let me add a few words. Imagine the tangent space of a manifold. We’d like a set of basis vectors for this tangent space. Of course, whatever basis we’re using for the manifold induces a basis on the tangent space, but let’s be more general. Let us write down an arbitrary basis. Each basis vector has 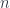n components, where 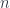n is the dimensionality of the manifold. Thus each basis vector gets an undex from 1 to 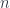n, which we call 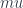mu. The choice of this label is intentional, the components of this basis map directly (say, by exponentiation) to the manifold itself, so these really are indices relative to the basis on the manifold. We can thus write a particular basis vector of the tangent space at x as e_\mu(x). 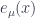How many basis vectors are there for the tangent space? There are 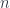n. We can thus label the different basis vectors with another letter, a. 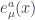Hence we may write our vector as e^a_\mu(x).

The point, now, is that these objects allow us to convert from manifold coordinates to tangent space coordinates. (Tautological sanity check: the a are tangent space coordinates because they label a basis for the tangent space.) In particular, we can go from the curved-space indices of a warped spacetime to flat-space indices that spinors understand. The choice of an orthonormal basis of tangent vectors means that

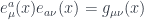e^a_\mu (x) e_{a\nu}(x) = g_{\mu\nu}(x),

where the a index is raised and lowered with the flat space (Minkowski) metric. In this sense the vielbeins can be thought of as `square roots’ of the metric that relate flat and curved coordinates. (Aside: this was the first thing I ever learned at a group meeting as a grad student.)

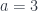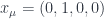Now here’s the good stuff: there’s nothing `holy’ about a particular orientation of the vielbein at a particular point of spacetime. We could have arbitrarily defined the tangent space z-direction (i.e. a = 3, not $\mu=3$) pointing in one direction (x_\mu=(0,0,0,1)) or another (x_\mu=(0,1,0,0)) relative to the manifold’s basis so long as the two directions are related by a Lorentz transformation. Thus we have an SO(3,1) symmetry (or whatever symmetry applies to the manifold). Further, we could have made this arbitrary choice independently for each point in spacetime. This means that the symmetry is local, i.e. it is a gauge symmetry. Indeed, think back to handy definitions of gauge symmetries in QFT: this is an overall redundancy in how we describe our system, it’s a `non-physical’ degree of freedom that needs to be `modded out’ when describing physical dynamics.

Like any other gauge symmetry, we are required to introduce a gauge field for the Lorentz group, which we shall call 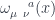\omega_{\mu\phantom{a}\nu}^{\phantom{mu}a}(x). From the point of view of Riemannian geometry this is just the connection, so we can alternately call this creature the spin connection. Note that this is all different from the (local) diffeomorphism symmetry of general relativity, for which we have the Christoffel connection.

What do we know about the spin connection? If we want to be consistent with general relativity while adding only minimal structure (which GSW notes is not always the case), we need to impose consistency when we take covariant derivatives. In particular, any vector field with manifold indices (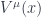V^\mu(x)) can now be recast as a vector field with tangent-space indices (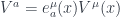V^a = e^\mu_a(x)V^\mu(x)). By requiring that both objects have the same covariant derivative, we get the constraint

D_\mu e^a_\mu(x) = 0.

Note that the covariant derivative is defined as usual for multi-index objects: a partial derivative followed by a connection term for each index. For the manifold index there’s a Christoffel connection, while for the tangent space index there’s a spin connection:

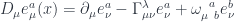D_\mu e^a_\mu(x) = \partial_\mu e^a_\nu - \Gamma^\lambda_{\mu\nu}e^a_\nu + \omega_{\mu\phantom{a}b}^{\phantom\mu a}e^b_\nu.

This turns out to give just enough information to constrain the spin connection in terms of the vielbeins,

\omega^{ab}_\mu = \frac 12 g^{\rho\nu}e^{[a}_{\phantom{a}\rho}\partial_{\nu}e^{b]}_{\phantom{b]}\nu}+ \frac 14 g^{\rho\nu}g^{\tau\sigma}e^{[a}_{\phantom{[a}\rho}e^{b]}_{\phantom{b]}\tau}\partial_{[\sigma}e^c_{\phantom{c}\nu]}e^d_\mu\eta_{cd},

this is precisely equation (11) of hep-ph/980547 (EFT for a 3-Brane Universe, by Sundrum) and equation ( 4.28 ) of hep-ph/0510275 (TASI Lectures on EWSB from XD, Csaki, Hubisz, Meade). I recommend both references for RS model-building, but note that neither of them actually explain where this equation comes from (well, the latter cites the former)… so I thought it’d be worth explaining this explicitly. GSW makes a further note that the spin connection can be using the torsion since they are the only terms that survive the antisymmetry of the torsion tensor.

Going back to our original goal of putting fermions on a curved spacetime, in order to define a Clifford algebra on such a spacetime it is now sufficient to consider objects 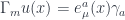\Gamma_mu(x) = e^a_\mu(x)\gamma_a, where the right-hand side contains a flat-space (constant) gamma matrix with its index converted to a spacetime index via the position-dependent vielbein, resulting in a spacetime gamma matrix that is also position dependent (left-hand side). 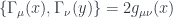One can see that indeed the spacetime gamma matrices satisfy the Clifford algebra with the curved space metric, \{\Gamma_\mu(x),\Gamma_\nu(y)\} = 2g_{\mu\nu}(x).

There’s one last elegant thought I wanted to convey from GSW. In a previous post we mentioned the role of topology on the existence of the (quantum mechanical) spin representation of the Lorentz group. Now, once again, topology becomes relevant when dealing with the spin connection. When we wrote down our vielbeins we assumed that it was possible to form a basis of orthonormal vectors on our spacetime. A sensible question to ask is whether this is actually valid globally (rather than just locally). The answer, in general, is no. One simply has to consider the “hairy ball” theorem that states that one cannot have a continuous nowhere-vanishing vector field on the 2-sphere. Thus one cannot always have a nowhere-vanishing global vielbein.

Topologies that can be covered by a single vielbein are actually `comparatively scarce’ and are known as parallelizable manifolds. For non-parallelizable manifolds, the best we can do is to define vielbeins on local regions and patch them together via Lorentz transformations (`transition functions’) along their boundary. Consistency requires that in a region with three overlapping patches, the transition from patch 1 to 2, 2 to 3, and then from 3 to 1 is the identity. This is indeed the case.

Spinors must also be patched together along the manifold in a similar way, but we run into problems. The consistency condition on a triple-overlap region is no longer always true since the double-valuedness of the spinor transformation (i.e. the spinor transformation has a sign ambiguity relative to the vector transformation). If it is possible to choose signs on the spinor transformations such that the consistency condition always holds, then the manifold is known as a spin manifold and is said to admit a spin structure. In order to have a consistent theory with fermions, it is necessary to restrict to a spin manifold.

 

January 2, 2009

Renormalization as Dimensional Analysis

Posted by Sparticles under Field Theory
[2] Comments 

Today I’ll be reviewing P.M. Stevenson, “Dimensional Analysis in Field Theory,” Annals of Physics 132, 383 (1981). It’s a cute paper that helps provide some insight for the renormalization group.

A theory is a black box

A theory is a black box that we can shake to make predictions of physical observables.

We’ve already said a few cursory words on dimensional analysis and renormalization. It turns out that we can use simple dimensional analysis to yield some insight on the nature of the renormalization group without having to think about the technical ‘heavy machinery’ required to do actual calculations.

First let us define a theory as a black box that is characterized by a Lagrangian and its corresponding parameters: coupling constants, masses, fields, etc. All these things, however, are contained within the black box and are in some sense abstract objects. One can ask the black box to predict physical observables, which can then be measured experimentally. Such observables could be cross sections, ratios of cross sections, or potentials, as shown in the image above.

Let’s now restrict ourselves to the case of a `naively-scale-invariant’ or `naively-dimensionless’ theory, i.e. one where there are no couplings with mass dimensions. For example, \lambda\phi^4 theory or massless QCD. We shall further restrict to dimensionless observables, such as the ratio of cross sections. Let’s call a general observable \rho(Q), where we have inserted a dependence on the energy Q with foresight that such things renormalize with energy scale.

Dimensional Analysis

But one can immediately take a step back and realize that this is ridiculous. How could a dimensionless observable from a dimensionless theory have a nontrivial dependence on a dimensionful quantity, Q? Stevenson makes this more explicit by quoting a theorem of dimensional analysis:

Thm. A function f(x,y) which depends only on two massive variables x,y and which is

  1. dimensionless
  2. uniquely defined
  3. defined without any dimensionful constants

must then be a function of the ratio of x/y only, f(x,y)=f(x/y).

Cor. If f(x,y) is independent of y, then f(x,y) is constant.

Then by the corollary, \rho(Q) must be constant. This is a problem, since our experiments show a Q dependence.

Evading Dimensional Analysis

The answer is that the theorem doesn’t hold: the theory inside the black box is not `uniquely defined,’ violating condition 2. This is what we meant by the stuff inside the black box being `abstract,’ the Lagrangian is actually a one-parameter family of theories with different bare couplings. That is to say that the black box is defined up to a freedom in the renormalization conditions.

Now that we see that it is possible to have Q-dependence, it’s a bit of a curiosity how our dimensionless theory manages to define a dimensionful dependence of \rho without any dimensonful quantities to draw upon. The simplest way to do this is to have the theory define the first derivative:

\frac {d\rho}{dQ} = \frac{1}{Q} \beta(\rho),

where \beta is the usual beta function calculated in perturbation theory. It is dimensionless and is uniquely defined by the theory. Another way one can define Q dependence is to do so recursively; one can read Stevenson’s paper to see that this is equivalent to defining the \beta function.

One can integrate the equation for \beta to write,

\log Q + constant = \int^\rho_{-\infty} \frac{d\rho'}{\beta(\rho)} \equiv K(\rho).

The constant of integration now characterizes the one-parameter ambiguity of the theory. (The ambiguity can be mapped onto the lack of a boundary condition.) We may parameterize this ambiguity by writing

constant = K_0 - \log \mu,

for some arbitrary \mu of mass dimension 1. (This form is necessary to get a dimensionles logarithm on the left-hand side.) The appearance of this massive constant is something of a `virgin birth’ for the naively-dimensionless theory and is called dimensional transmutation. By setting Q=\mu we see that K_0 = K(\rho(\mu)). Thus we see finally that the integral of the \beta equation is

\log(Q/\mu) + K(\rho(\mu)) = K(\rho(Q)).

All of the one-parameter ambiguity of the theory is now packaged into the massive parameter \mu. K is an integral that comes from the \beta function, which is in turn specified by the Lagrangian of the theory. On the left-hand side we have quantities which depend on the arbitrary scale \mu while the right-hand side contains only quantities that depend on the energy scale Q.

If K(\rho(\mu)) vanishes for some \mu=\Lambda, then we can write our observable in terms of this scale,

\rho(Q) = K^{-1}(\log(Q/\Lambda)).

Note that \mu is arbitrary, while \Lambda is fixed for a particular theory. This latter quantity is rather interesting because even though it is an intrinsic property of the black box, it is not predicted by the black box, it must be fixed by explicit measurement of an observable. (more…)

 

December 19, 2008

Why renormalize? A discussion in words.

Posted by Sparticles under Field Theory
[3] Comments 

For various reasons I’ve been having fun thinking about renormalization, so I thought I’d try to put together a post about renormalization in words (rather than equations).

The standard canon for field theory students learn is that when a calculation diverges, one has to (1) regularize the divergence and then (2) renormalize the theory. This means that one has to first parameterize the divergence so that one can work with explicitly finite quantities that only diverge in some limit of the parameter. Next one has to recast the entire theory for self-consistency with respect to this regularization.

While there are some subtleties involved in picking a regularization scheme, we shall not worry about this much and will instead focus on what I think is really interesting: renormalization, i.e. the [surprising] behavior of theories as one changes scale.

The details of the general regularization-renormalization procedure can be found in every self-respecting quantum field theory textbook, but it can often be daunting to understand what’s going on physically rather than just technically. This is what I’d like to try to explore a bit.

First of all, renormalization is something that is intrinsically woven into quantum field theory rather than a `trick’ to get sensible results (as was often said in the 1960s). One way of looking at this is to say that we do not renormalize because our calculations find infinities, but rather because of the nature of quantum corrections in an interacting theory.

Recall the Lehmann-Symanzik-Zimmerman (LSZ) reduction procedure. Ha ha! Just kidding, nobody remembers the LSZ reduction formalism unless they find themselves in the unenviable position of teaching it.

Here’s what’s important: we understand the properties of free fields because their Lagrangian is quadratic and the path integral can be solved explicitly. But non-interacting theories are boring, so we usually play with interacting theories as perturbations on free theories. When we do this, however, things get a little out-of-whack.

Statements about free field propagators, for example, are no longer strictly true because of the new field interactions. The two-point Greens function is no longer the simple propagator of a field from one point to another, but now takes into account self-interactions of the field along the way. This leads one to the Lehmann-Kallen form of the propagator and the spectral density function which encodes intermediate bound states.

You can go back and read about those things in your favorite QFT text, but the point is this: we like to use “nice” properties of the free theory ito work with our interacting theory. In order to maintain these “nice properties” we are required to rescale (renormalize) our fields and couplings. For example, we would like to maintain that a field’s propagator has a pole of unity residue at its physical mass, the field operator annihilates the vacuum, and that the field is properly normalized. Assuming these properties, the LSZ reduction procedure tells us that we can calculate S-matrix elements in the usual way.

Suppose we start with a model, represented by some Lagrangian. We call this the bare Lagrangian. This is just something some theorist wrote down. The bare Lagrangian has parameters (masses, couplings), but they’re “just variables” — i.e. they needn’t be `directly’ related to measurable quantities. We rescale fields and shift couplings to fit the criteria of LSZ,

\phi = Z^{-1/2}\phi_{bare}
g = g_{bare} + \delta g.

We refer to these as the renormalized field and renormalized couplings. These quantities are finite and can be connected to experiments.

When we do calculations and find divergences, we can (usually) absorb these quantities into the bare field and couplings. Thus the counter terms \delta g and the field strength renormalization Z are also formally divergent, but in a way that cancels the divergence of the bare field and couplings.

That sets everything up for us. We haven’t really done anything, mind you, just set up all of the clockwork. In fact, the real beauty is seeing what happens when we let go and see what the machine does (the renormalization group). I’ll get to this in a future post.

Further reading: For beginning field theorists, I strongly recommend the heuristic description of renormalization in Zee’s QFT text. A good discussion of LSZ and the Lehmann-Kallen form is found in the textbooks by Srednicki and Ticciati. Finally, for one of the best discussions of renormalization, the Les Houches lectures “Methods in Field Theory” (a paperback version is available for a reasonable price) is fantastic.

 

December 10, 2008

Two component spinors, a comprehensive guide

Posted by Sparticles under Field Theory
Comments Off on Two component spinors, a comprehensive guide 

Today a new paper by Dreiner, Haber, and Martin has me really excited: “Two-component spinor techniques and Feynman rules for quantum field theory and supersymmetry,” arXiv:0812.1594. It appears to be a comprehensive (246 page) guide to working with two-component Weyl fermions.

Most quantum field theory texts of the 90s (i.e. Peskin and Schroeder) used four-component Dirac spinors. The primary motivation for this is that Dirac spinors are the irreducible representations of massive fermions. Weyl spinors, however, are mathematically the fundamental representations of the universal cover of the Lorentz group. (See our previous post on spinors.) The fermionic generators of supersymmetry, for example, are Weyl spinors.

More practically, two-component Weyl spinors are easier to work with than four-component Dirac spinors… by a factor of two—see how I did some tricky math, there? Instead of working with \gamma-matrices in some representation, one can work with \sigma-matrices (Pauli matrices) which have a single standard representation. The “gamma gymnastics” of calculations thus becomes simpler.

Most importantly, each Weyl fermion corresponds to a chiral state. This is arguably (i.e. for everyone but experimentalists) the most sensible representation because the Standard Model is a chiral theory. (We’ve got a previous post on this point, too.) Thus working with the two-component fermions give a better handle for the actual physics at hand; i.e. less confusion about chirality versus helicity, no more need for chiral projectors in Feynman rules, etc.

Of course, this all comes at a cost. One has to relearn the spinor formalism. Feynman rules have to be rewritten with different conventions for arrows and mass terms. (Recall that the mass terms are what mix the left- and right-chiral Weyl spinors into a propagating Dirac spinor.) Fortunately, the guide has ample worked examples to help get students up-and-running.

I’ve often heard more senior physicists bemoan the fact that we teach QFT using four-component spinors just because that’s what everyone else uses. They quote the absence of a thorough and unambiguous treatment of QFT using two-component spinors to once-and-for-all encourage the community to make a phase transition to a new vacuum. Well, I’m not sure if this will be the treatment that leads the revolution, but I know that I’ll certainly keep it handy.

The guide comes with a webpage that contains an alternate version using the GR/East-coast/mostly-plus metric. (Because if particle physicists are finaly breaking free of Dirac spinors, we might as well get rid of our metric as well…?) Stephen Martin has also updated his famous SUSY Primer to utilize Weyl spinors and the ‘subversive’ metric, along with a few content updates.

Boy, the department printer is sure going to get a work out this afternoon.

 

December 1, 2008

Chirality and BSM

Posted by Sparticles under BSM, Field Theory
[2] Comments 

Is it just me or does fermion chirality play a big role in beyond the standard model physics?

The Standard Model is a chiral theory; left- and right-handed fermions (i.e. -/+ eigenstates of the chirality operator \gamma_5) live in different representations of the SM gauge group. This poses a rather rigid constraint on what kind of model becomes effective at the TeV scale.

Chirality prevents the use of low-scale models with multiple supersymmetries (\mathcal N>1), since this means one would be able to take a spin +1/2 fermion \psi and expect to find a spin -1/2 fermion Q_1Q_2\psi in the same supermultiplet (i.e. with the same gauge quantum numbers).

In extra dimensional models, the lack of a chiral operator in 5 dimensions (and more generally for most higher dimensions) stunted the development of KK models until the 80s. In a nutshell, there exists no chirality operator in five dimensions (\gamma_5 is just an ‘ordinary’ gamma matrix) and hence all fermions are Dirac rather than Weyl. This has led to lots of work with orbifolds and boundary conditions. [It might be neat to think about how such boundary conditions for different backgrounds could come from string theory.]

Even in lattice field theory, there is a “Nielsen Ninomiya No-Go” theorem for chiral fermions. (“No-Go Theorum for Regularizing Chiral Fermions [sic.]”)

I wonder if there are still novel ways to get chiral fermions from these theories that are just waiting for a clever model-builder to figure out?

 

November 28, 2008

Why spinors?

Posted by Sparticles under Field Theory
[2] Comments 

Spinors are somewhat subtle objects in field theory. They are our mathematical representation of fermions, which are spin-1/2 objects, and hence have the unintuitive property that a 2\pi rotation does not return them to their initial state, but a 4\pi relation does. (For a classical analogue, see Bolker’s spinor spanner.) Any quantum field theory text will teach how to manipulate spinors… but it’s not always made clear where spinors come from in the first place.

Here I’d like to say a few introductory words on the spin representation. I’ll assume a background in representations of Lie groups but will try to be very qualitative. For a proper introduction, see Weinberg Vol. I section 2.7.

Even before learning group theory physics students have an intuition for vector and tensor representations of the Lorentz algebra, SO(3,1). These are just the usual objects with indices in special and general relativity. These correspond to the usual fundamental and tensor reps that one constructs for a general Lie algebra. Classically, those are all the reps that we would expect nature could choose from.

But alas, our universe is not filled with only vectors and scalars. We also observe fermions, which are not spin-1 or spin-0, but rather spin-1/2. The spin-1/2 representation is inherently quantum in origin (and this is the part that I think is really neat).

In quantum mechanics an object’s state is given by its wavefunction, \psi(x,t). This is a complex number that can be decomposed into an magnitude and a phase. Physical observables, however, are given only by the magnitude of the wavefunction and are independent of the phase. Relative phases can, of course, produce physical effects; but we’re focusing on one-particle states.

This independence on the phase allows us to relax our restrictions on the representation of a group on quantum states. Usually we require that elements of a lie group/algebra g_1,g_2 are represented by matrices U(g_1), U(g_2) with the property (by the definition of a representation) that

U(g_1) U(g_2)=U(g_1g_2).

In quantum mechanics, however, we have the freedom to allow the product of representations to introduce a phase. That is to say, acting on a wavefunction \psi, our representation permits a \theta such that

U(g_1) U(g_2) \psi = U(g_1g_2)e^{i\theta(g_1,g_2)}\psi.

These representations “up to a phase” are called projective representations. Neat. But so what?

It turns out that it’s actually rather difficult to construct projective representations of a group/algebra. In fact, most groups don’t even permit projective representations — attempts to write a projective representation can be rewritten in terms of `normal’ representations.

One sufficient condition for a group to furnish a projective rep is that the group is not simply connected. We’ll leave it at this with no further proof, but it is rather cute that the quantum properties of a group’s representation can depend on its topology.

The point is that the Lorentz group is not simply connected, and hence it permits projective representations. This projective representation corresponds to the spinor rep. One can get a flavor of this by noting that the Loretnz group is doubly connected. This is the source of the rotation-by-4\pi property of spinors.

To complete the story, we note that it also turns out that instead of working with projective representations of a group, one can equivalently work with regular representations of the universal covering of that group. Practically, this means that instead of working with the Lorentz group, SO(3,1) = SL(2,C)/Z_2 we work with the simply connected group SL(2,C). The fundamental representations are the very Weyl spinors that we know and love.

Further Reading

For a more rigorous treatment of the above discussion see Weinberg, Vol I section 2.7. There are many more interesting things to learn about spinors. Spinors in higher dimensions are treated in Polchinski, Vol II appendix B. There’s a very nice relation between the Clifford algebra in arbitrary dimension and differential forms. See appendix A of hep-th/0510176 and the references therein. A proper mathematical treatment require deciphering the statement “spinor representations are the square root of a principle fiber bundle,” I suppose a good place to start is Nakahara, but probably the place to go is Kobayashi and Nomizu. [This is something I’d like to learn more about… maybe I could toss around the idea of an informal reading group with some of the students next semester.]